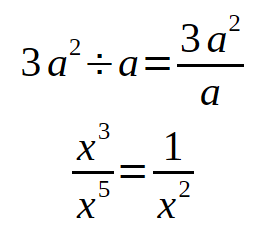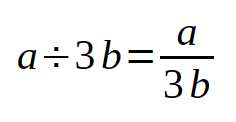In this lesson, let’s look at how to represent notations in algebra.
4 Operations of Algebra
Addition and Subtraction
In algebra, we can only add or subtract like terms together.
Examples:
a + a = 2a
6a + a = 7a
7b – b = 6b
10b -3b = 7b
We cannot add or subtract unlike terms.
E.g. x + y is still x+ y, we cannot combine x and y in anyway since they are not the same.
Think of adding the number of chickens to the number of ducks. The number of chickens and ducks still remain the same.
More examples:
2x + 5y = 2x + 57
2x + y + 6y – x = 2x-x + y + 6y = x + 7y
6xy + 2y -3x = 6xy + 2y -3x (note that the terms must be the same, xy, x and y are all unlike terms and cannot be combined together by addition or subtraction)
3x³ + 2x + 5x + 2 + 3 = 3x³ + 7x + 5 (the numbers i.e. 2 and 3 can be added together. The terms containing x i.e. 2x and 5x can also be added together. However, x³ is not like term as x, and they cannot be combined together in addition or subtraction)
Multiplication
To represent multiplication, we can combine the different terms together and take away the × sign.
Examples:
a × b = ab
3a × 2y = 6ay
The bracket sign is sometimes used to represent multiplication.
Example:
c × d = (c)(d) –> Although we usually write this as just cd
The bracket sign is usually used when we are multiplying a group of algebraic terms together.
Examples:
3 × (x+y) = 3(x+y)
(x-3) × (x+5) = (x-3)(x+5)
When we multiply like terms together, the power changes. Think of the power as “repeated multiplication” or how many times a term is multiplied by itself.
Example:
a x a = a²
a x a x a = a³
a x a² = a³
Division
We often use fraction to represent division in algebra:
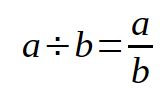
More examples:
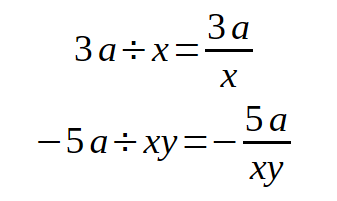
When we divide terms with the same base together, the power changes.
Examples: