Inequalities are mathematical statements that compare two values, showing that one number is greater than, less than, or sometimes equal to another number. Instead of using the equal sign “=”, inequalities use symbols such as:
- > (greater than),
- < (less than),
- ≥ (greater than or equal to)
- ≤ (less than or equal to)
- ≠ (not equal to)
Inequalities are very common in mathematics because many situations do not have one exact value. For example, a person must be at least 13 years old to create a certain social media account. That means the age is 13 and above or ≥13. This idea of comparing and setting boundaries is the foundation of inequalities.
Inequalities and some “common” words
Here are some words that you’ll see very commonly when setting up inequalities:
| Key Words | Inequality Sign to use |
| more (greater) than | > |
| more (greater) than or equal to | ≥ |
| less than | < |
| less than or equal to | ≤ |
| at most | ≤ |
| not more than | ≤ |
| at least | ≥ |
| not less than | ≥ |
| not equal to | ≠ |
Inequalities and the Number Line
A number line helps us clearly show which values are included in an inequality. When we place an inequality on a number line, we first mark the point where the number is located, then draw a line or shading in the direction that shows the range of solutions.
We also, put a circle around some numbers on the number line. The circle can be an open circle ,○, or closed circle, ●:
| Symbol | What is means |
| ○ | the number is not included |
| ● | the number is included |
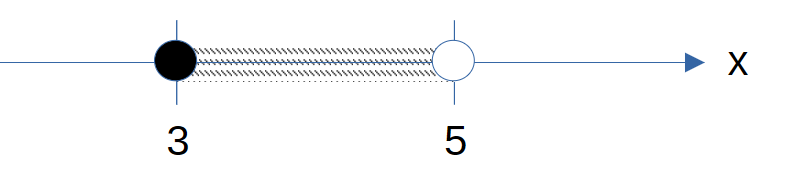
Example 1: Represent x > 5 on the number line.

Example 2: Represent x ≥ 5 on the number line.

Example 3: Represent x< 5 on the number line.
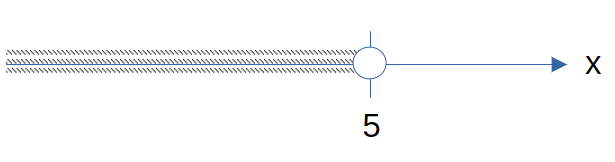
Example 4: Represent x≤ 5 on the number line.
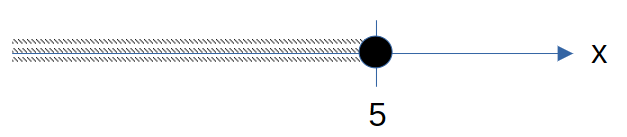
Example 5: Represent 3<x< 5 on the number line.
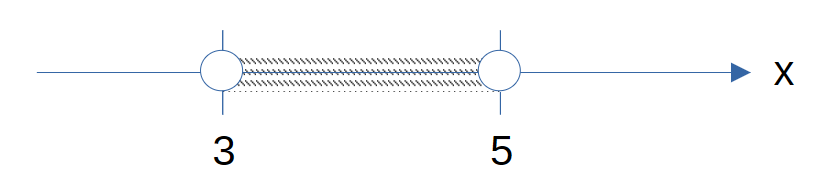
Example 6: Represent 3≤x< 5 on the number line.