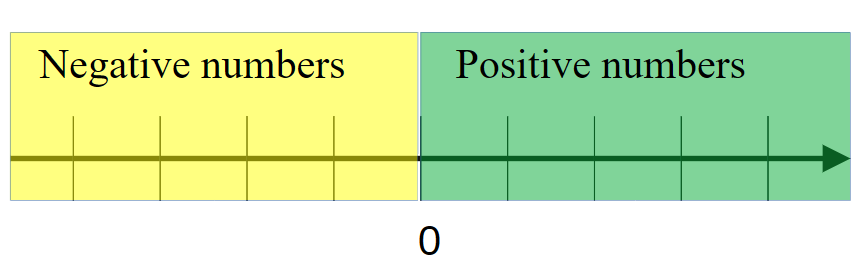
Negative numbers are numbers less than zero, written with a minus sign (−).
In this lesson, we’ll look at:
- Comparing Negative Numbers
- Four Operations of Negative numbers
Comparing Negative Numbers
Negative numbers are less than 0. Hence, a negative number will always be smaller than any positive number or 0.
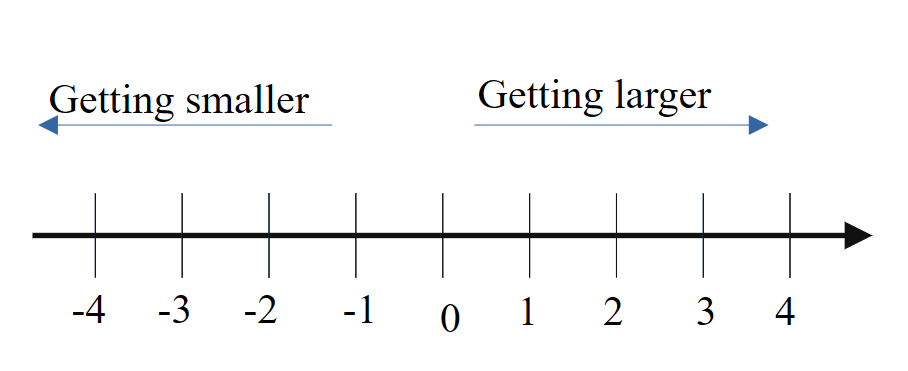
When represented on a number line, negative numbers are found on the left of 0, while positive numbers are found on the right of 0.
Example: -3 < 0.1
Example: -1000 < 0
The more negative a number is, the further it lies to the left on the number line, making it smaller in value. For example, -3 lies more to the left than -1 on the number line, hence -3 < -1.
Four Operations of Negative Numbers
Addition involving negative numbers
Adding a negative number to a positive number is like subtraction.
Example: 5 + (-3) = 5 -3 = 2
Example: -6 +9 = 9 – 6 = 3
Example: 5-7 = -2
If we are adding 2 negative numbers, it should become more negative.
Example: -5 -3 = -8
Subtraction involving negative numbers
Subtracting a negative number is the same as adding a positive number. Or simply remember, — = +
Example: 7 – (-2) = 7 + 2 = 9
Multiplication involving negative numbers
- Multiplying a negative number by a positive number (or an odd number of negative numbers) gives a negative result.
Example: -3 x 2 = -6
Example: -3 x 4 x -2 x -1 = -24 (since there are 3 negative numbers in the multiplication, and 3 is odd, the result is negative)
- Multiplying two negative numbers (or an even number of negative numbers) gives a positive result.
Example: -2 x -3 = 6
Example: -2 x -2 x -4 x 3 x -1 = 48 (since there are 4 negative numbers in the multiplication, and 4 is even, hence the result is positive)
Division involving negative numbers
Division follows the same rule as multiplication.
- If 1 number in the division is negative and the other is positive, the result is negative.
Example: 6 ÷ (-2) = -3
Example: -8 ÷ 4 = -2
- If both numbers in the division are negative, then the result is positive.
Example: -8 ÷ (-2) = 4
