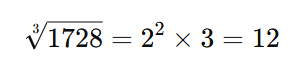In this lesson, we’ll look at how to apply prime factorisation to find:
- lowest common multiple (LCM)
- Highest common factor (HCF)
- Square roots
- Cube Roots
Using Prime Factorisation to find Lowest Common Multiple (LCM)
A multiple of a number is what you get when you multiply that number by a whole number (1, 2, 3, 4, …).
The Lowest Common Multiple (LCM) of two or more numbers is the smallest number that is a multiple of all of them.
In primary school, we list out the multiples of the numbers to find the lowest common multiple (see Example 1). This method is often used when the numbers are relatively small, and we do not need to list a huge list of numbers before finding the LCM.
Example 1: Find the common multiple of 2 and 5:

In secondary school, we find the lowest common multiple using prime factorisation. This method is easier when dealing with large numbers or when the LCM is not one of the first few multiples.
How to find the lowest common multiple (LCM) using prime factorisation
Step 1: Write each number as a product of their prime factors
Step 2: Identify ALL the prime factors that appear
Step 3: For each prime factor, take the highest power that appears.
Step 4: Multiply them together.
Example 2: Find the Lowest Common Multiple (LCM) of 720 and 23625.
Step 1: Let’s write 720 and 23625 as product of their prime factors.
720 = 2⁴ x 3² x 5
23625 = 3³ x 5³ x 7
Step 2: Identify ALL the prime factors that appear.
From the prime factorisation of 720 and 23625, the prime factors that appear for both numbers are : 2, 3, 5 and 7.
Step 3: For each prime factor, take the highest power that appears.
For 2, the highest power is 4.
For 3, the highest power is 3.
For 5, the highest power is 3.
For 7, the highest power is 1.
Step 4: Multiply them together.
Hence, the LCM of 720 and 23625 = 2⁴ x 3³ x 5³ x 7 = 378,000
Using Prime Factorisation to find Highest Common Factor (HCF)
A factor of a number is a number that divides it exactly (without leaving any remainder).
For example, the factors of 12 are 1, 2, 3, 4, 6 and 12.
The Highest Common Factor (HCF) of two or more numbers is the largest number that divides all of them exactly.
In Primary school, we find the highest common factor by listing all the factors of the numbers, and then selecting the largest factor that is common to these numbers.
Example 3: Find the Highest Common Factor (HCF) of 24 and 36:

In secondary school, we often use prime factorisation to find the highest common factor (HCF).
How to find Highest Common Factor (HCF) using Prime Factorisation
Step 1: Write each number as a product of prime numbers.
Step 2: Identify the common prime factors.
Step 3: Take the lowest power of each factor.
Step 4: Multiple them together.
Example 4: Find the Highest Common Factor of 72 and 80 by Prime Factorisation.
Step 1: Write both 72 and 80 as product of their prime factors.
72 = 2³ x 3²
80 = 2⁴ x 5
Step 2: Identify the common prime factors.
Both 72 and 80 have 2 as the common prime factor.
Step 3: Take the lowest power.
The lowest power of 2 is 3.
Step 4: Multiply them together.
The lowest common factor of 72 and 80 = 2³ = 8
Using Prime Factorisation to find Square Roots
The square root of a number is a value that, when multiplied by itself, gives the original number.
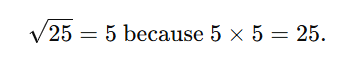
How to find square root of a number using prime factorisation
Step 1: Write the numbers as a product of its prime factors.
Step 2: Divide the power of each prime factor by 2.
Step 3: Multiply them together.
Example 5: Find the square root of 784.
Step 1: Write 784 as a product of its prime numbers.
784 = 2⁴ x 7²
Step 2: Divide the power of each prime factor by 2.
The power of 2 is 4. 4 ÷ 2 = 2.
The power of 7 is 2. 2÷2 = 1.
Step 3: Multiply them together.
√784 = 2² x 7 = 28
Using Prime Factorisation to find Cube Roots
The cube root of a number is a value that, when multiplied by itself three times, gives the original number.

How to find cube root of a number using prime factorisation
Step 1: Write the numbers as a product of its prime factors.
Step 2: Divide the power of each prime factor by 3.
Step 3: Multiply them together.
Example 6: Find the cube root of 1728.
Step 1: Write the numbers as a product of its prime factors.
1728= 2⁶ x 3³
Step 2: Divide the power of each prime factor by 3.
The power of 2 is 6. 6 ÷ 3 = 2.
The power of 3 is 3. 3 ÷ 3 = 1.
Step 3: Multiply the numbers together.